문제
leetcode.com/problems/maximum-product-subarray/
Maximum Product Subarray - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
코드
class Solution {
func maxProduct(_ nums: [Int]) -> Int {
var minValue = nums[0]
var maxValue = nums[0]
var result = nums[0]
for i in 1..<nums.count {
var currValue = nums[i]
var tempMinValue = minValue * currValue
var tempMaxValue = maxValue * currValue
maxValue = max(currValue, tempMaxValue, tempMinValue)
minValue = min(currValue, tempMaxValue, tempMinValue)
result = max(maxValue, result)
}
return result
}
}설명
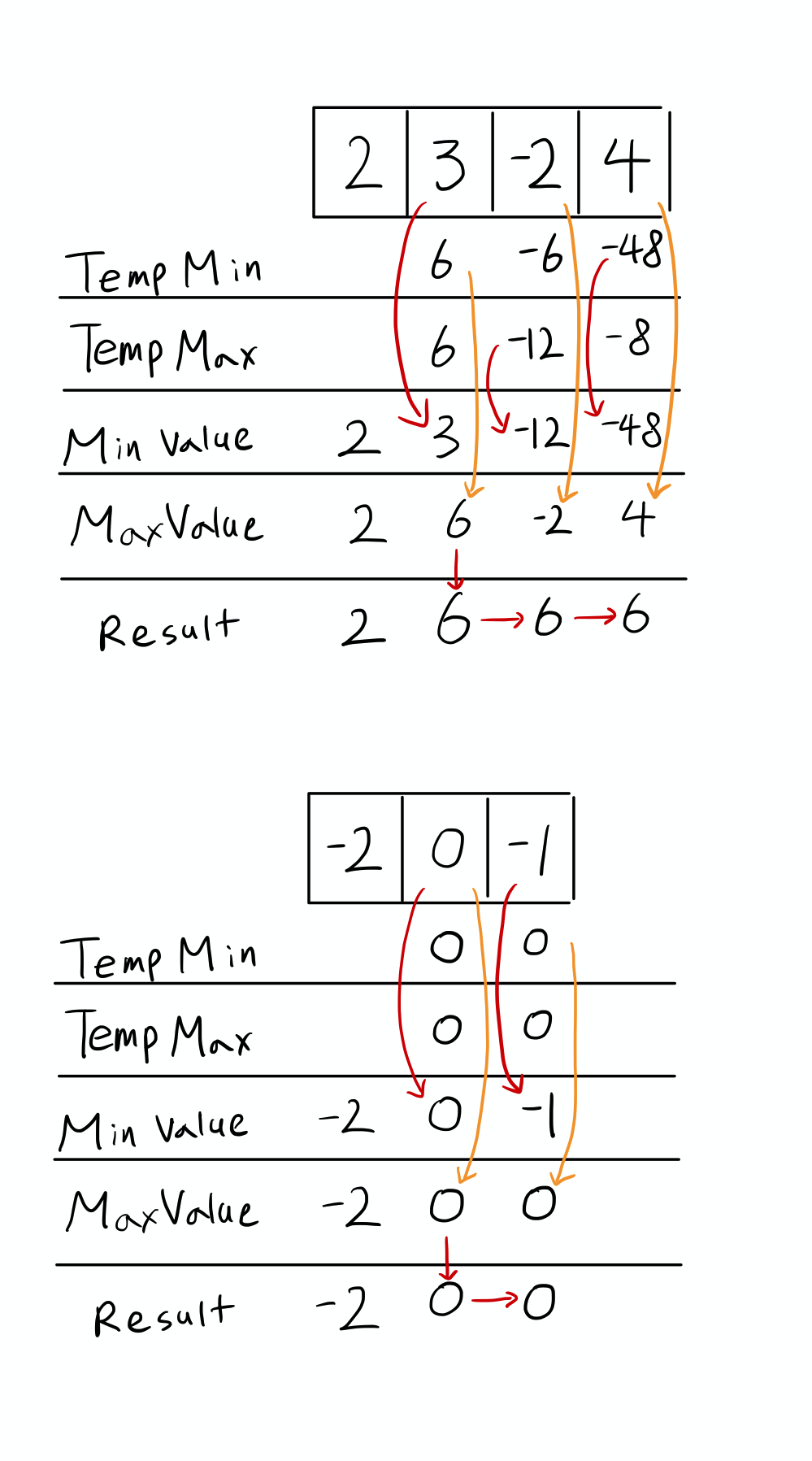
연속 합이 아닌 연속 곱의 문제입니다.
연속 합인 경우, 값이 극적으로 변하는 경우가 거의 없지만,
연속 곱의 경우, 음수 및 0을 통해 최소값이 최대값으로, 최대값이 최소값으로 변경되는 등 극적으로 변하는 경우가 발생합니다.
그래서 최소값과 최대값을 계산해가며 나아가야해요.
결국 우린 다음 3개의 값을 비교하고, 저장해야 해요
nums[k], minValue * nums[k], maxValue * nums[k]
3개의 값 비교를 통해, max 값을 저장하고, min 값을 저장해야 합니다.
또한, 우리의 목표는 연속 곱의 최대값이기 때문에, 계산한 max값을 비교하여, 최대값을 result 변수에 저장합니다.
회고
사실 처음 문제를 접근할 땐, 이중 포문으로 구현을 했고, 종료 타이밍에 대해서 집중했습니다.
0이 될 경우 더이상 곱셈 의미가 사라지기 때문에, 곱셈결과 0이 된 경우 더이상 계산하지 않는 방식으로 생각했는데,
1과 -1이 반복되는 배열에서 시간초과가 발생하더라구요.
이전문제에도 이중포문은 시간초과 발생하는 경우가 빈번했는데,
앞으로는 문제풀이에 있어서 이중 포문을 활용하는 로직에 대한 생각은 아예 버려야겠네요.

'코딩 테스트 > LeetCode(swift)' 카테고리의 다른 글
| [LeetCode] 33. Search in Rotated Sorted Array (0) | 2021.03.23 |
|---|---|
| [LeetCode] 153. Find Minimum in Rotated Sorted Array (0) | 2021.03.22 |
| [LeetCode] 53. Maximum Subarray (0) | 2021.03.20 |
| [LeetCode] 238. Product of Array Except Self (0) | 2021.03.20 |
| [LeetCode] 217. Contains Duplicate (0) | 2021.03.20 |



