문제
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규
www.acmicpc.net
잠깐만
2519. 계단 오르기 문제와 유사하네요
DP - 2579. 계단 오르기
문제 www.acmicpc.net/problem/2579 과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점" data-og-host="www.acmicpc.net" data-og-source-url="https://www.acmicpc.net/p..
skillist.tistory.com
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
long maxValue = 0;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int targetNum = Integer.parseInt(st.nextToken());
long[] before1 = new long[targetNum+1];
long[] before2 = new long[targetNum+1];
long[] before3 = new long[targetNum+1];
if (targetNum >= 1) {
st = new StringTokenizer(br.readLine());
int value = Integer.parseInt(st.nextToken());
before1[1] = value;
before2[1] = value;
before3[1] = value;
maxValue = value;
}
for (int n = 2; n <= targetNum; n++) {
st = new StringTokenizer(br.readLine());
int value = Integer.parseInt(st.nextToken());
before1[n] = value + Math.max(before2[n-1], before3[n-1]);
maxValue = Math.max(maxValue, before1[n]);
before2[n] = value + Math.max(Math.max(before1[n-2], before2[n-2]), before3[n-2]);
maxValue = Math.max(maxValue, before2[n]);
if (n >= 3) {
before3[n] = value + Math.max(Math.max(before1[n-3], before2[n-3]), before3[n-3]);
maxValue = Math.max(maxValue, before2[n]);
}
}
System.out.println(maxValue);
}
}
설명
2519. 계단 오르기와 같이 최대값을 계산하며 나아가는 로직입니다.
계단 오르기 문제와 다만 다른점이 있죠.
계단 오르기에선, 1칸 전진(연속으로 1칸 전진은 불가능)과 2칸 전진이 가능합니다.
하지만 우리가 풀어 볼 포도주 시식 문제는 "연속 3잔 마시기 불가능"이란 제약 조건만 있어요.
따라서, 계단 오르기와 같이, 1칸 전진(연속으로 1칸 전진 불가능), 2칸 전진, 3칸 전진이 가능합니다.
세칸이 핵심이에요. 세칸 전진하여 계산하는 경우가 있습니다.
다음 예제를 보실까요?
1칸 전진(연속으로 1칸 전진 불가능은 불가능) 제약 사항으로 발생한 케이스입니다.
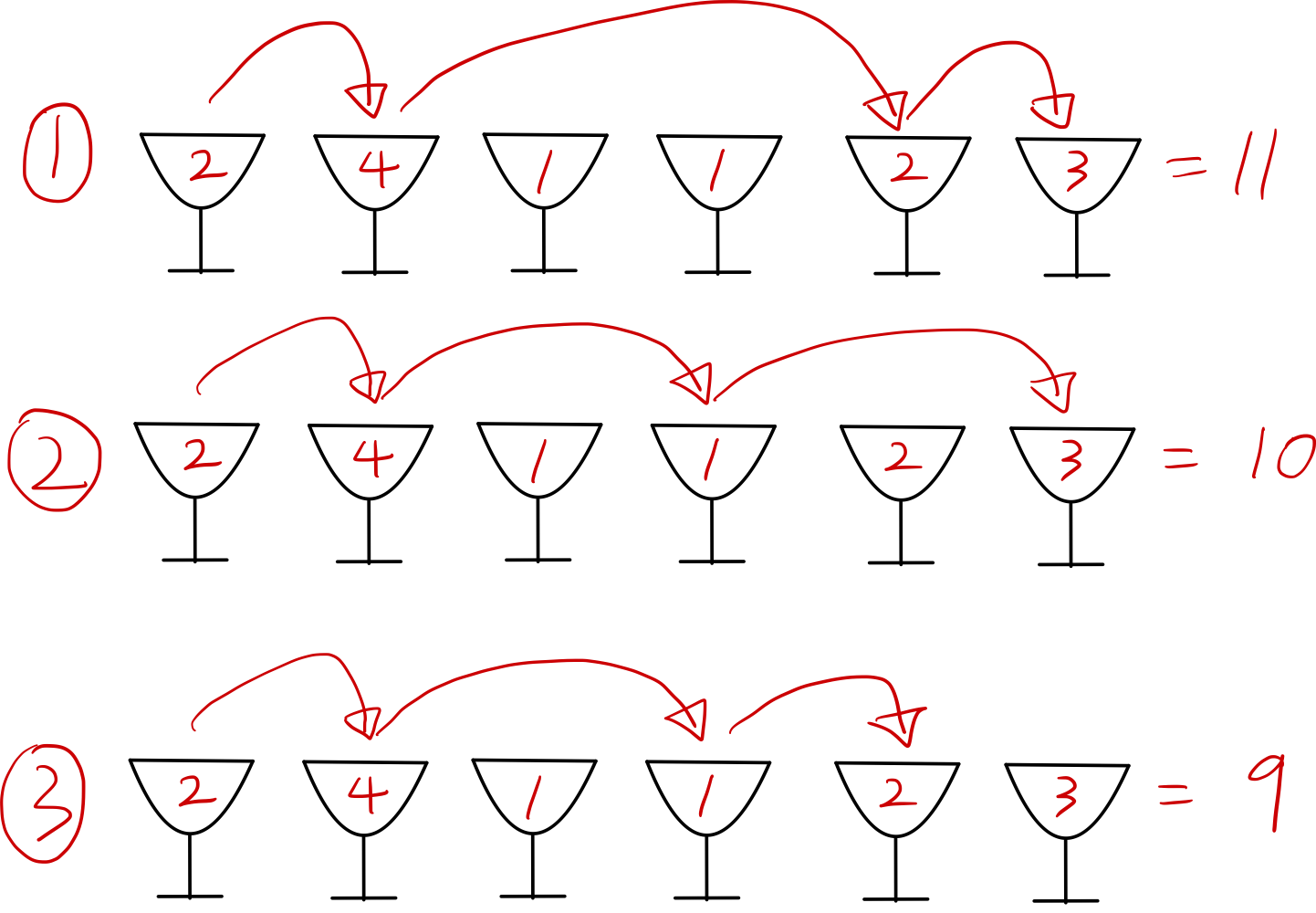
1번의 경우 3칸 전진하여(4 -> 2) 최대값은 11입니다.
2번의 경우 최대 2칸만 전진하여 최대값은 10입니다.
3번의 경우 최대 2칸만 전진하여 최대값은 9입니다.
따라서 세칸 전진도 계산해야해요.
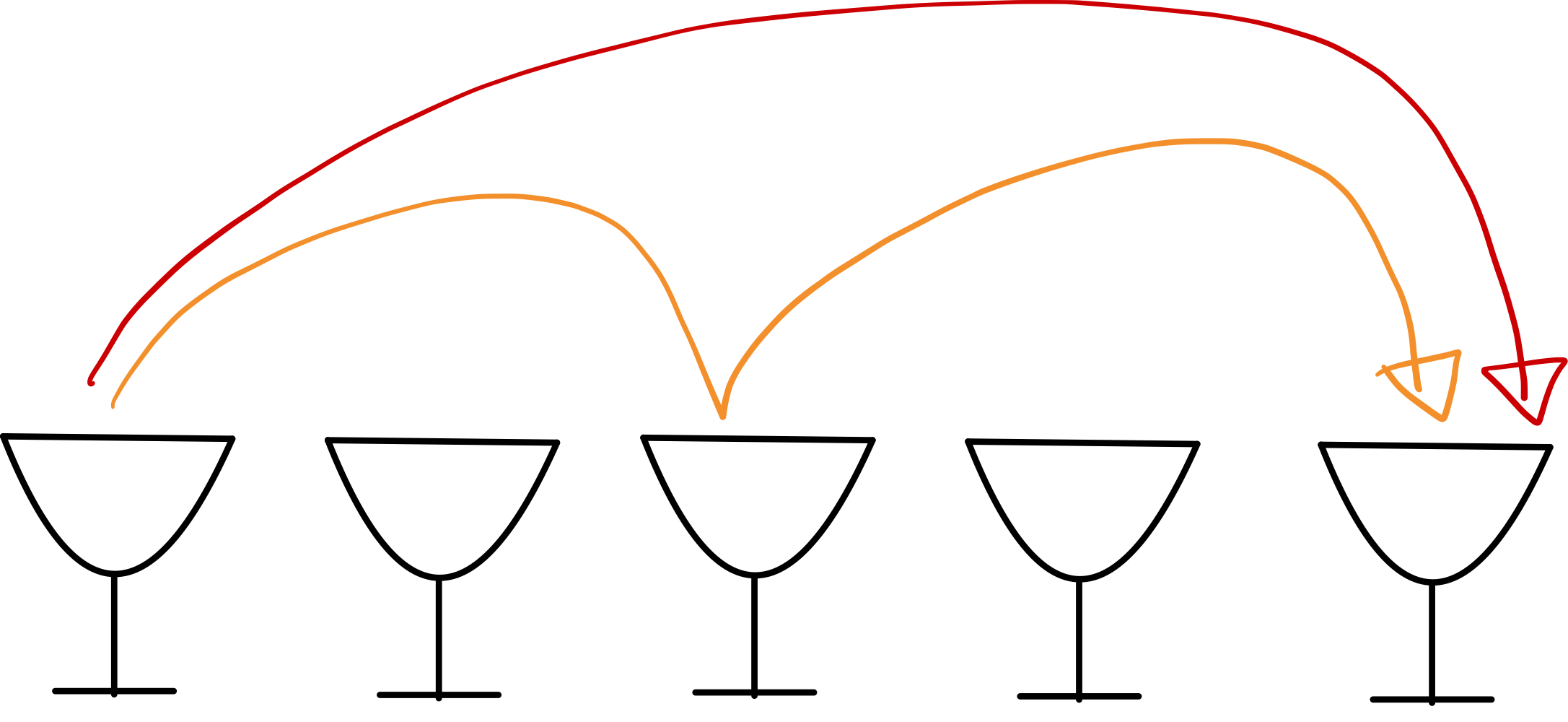
네칸 전진도 있지 않냐구요? 네. 네칸 전진도 있죠. 하지만, 네칸은 두칸 두칸씩 전진해서, 포도주 한잔이라도 더 먹으면 이익이잖아요?
"네칸 전진의 최대값 <= 두칸 두칸 전진의 최대값" 이므로, 네칸 이상부터는 계산할 필요가 없어집니다.
회고
세칸 전진을 생각하기까지 너무 오래 걸렸어요.
정답을 제출해도, 중간에 답이 틀렸다고 발생하는것만 봐도, 무언가를 놓치고 있는 느낌이었거든요.
해당 문제의 예제 수만 많았으면 좀 좋았을것 같은데, 이런점에서 아쉽네요.
'코딩 테스트 > 백준(java)' 카테고리의 다른 글
| DP - 2748. 피보나치 수 2 (0) | 2021.03.30 |
|---|---|
| DP - 11053. 가장 긴 증가하는 부분 수열 (0) | 2021.03.30 |
| DP - 10870. 피보나치 수 5 (0) | 2021.03.28 |
| DP - 1932. 정수 삼각형 (0) | 2021.03.27 |
| DP - 2579. 계단 오르기 (0) | 2021.03.27 |


